GIS复习【III】

文章较长，建议从目录选取感兴趣内容，然后Ctry+F搜索、跳转

6、空间数据模型*

数据模型是对现实世界进行认知、简化和抽象表达

空间实体抽象的三个层次

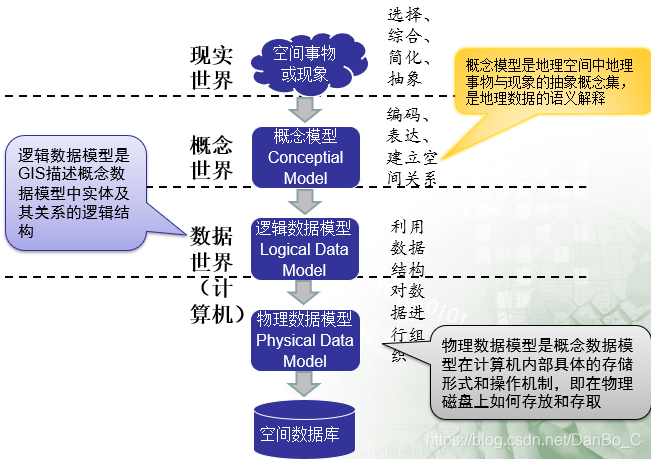
空间数据模型概念
- 对象模型
- 场模型
- 网络模型

空间逻辑数据模型
- 矢量数据模型
- 栅格数据模型
- 矢量-栅格一体化数据模型
- 镶嵌数据模型
- 面向对象数据模型

7、栅格数据结构**

概念

定义：将地表划分成为紧密相邻的网格阵列。每个网格的位置由行列号定义，并包含一个代码，以表示该网格的属性。

注意：栅格数据模型是将连续空间离散化，即用二维铺盖或划分覆盖整个连续空间。
特点
1. 属性明显，定位隐含；
2. 数据结构简单；
3. 面向位置的数据结构，难以建立空间对象之间的关系；
4. 比例尺大小为栅格(像元)的大小与地表相应单元的大小之比；存在几何和属性偏差。
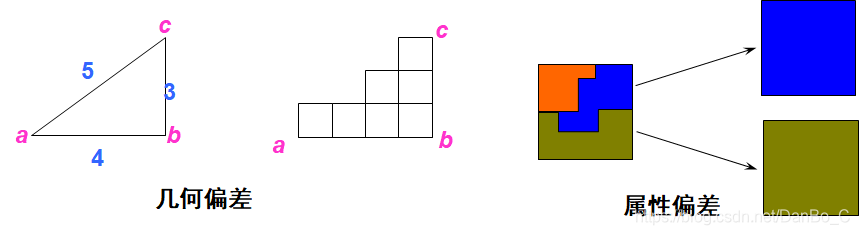
属性值的确定 x
1. 中心点法：取位于栅格中心的属性值为该栅格的属性值。
2. 面积占优法：栅格单元属性值为面积最大者。
3. 重要性法：取重要的属性值为栅格属性值。
4. 长度占优法：每个栅格单元的值由该栅格中线段最长的实体的属性来确定。
栅格结构数据获取的途径
- 手工获取
- 扫描仪扫描
- 遥感影像数据
- 由矢量数据转换而来
栅格数据编码方法**
1. 直接栅格编码
  
  优点：简单、直观，无压缩
  
  缺点：存在大量冗余，精度提高有限制。
  
  完全栅格数据的组织：基于层（波段）、基于行、基于像元。
2. 游程编码长度
  - 数据结构：（A，P），A表示属性值，P代表该游程相同代码重复的个数。
  - 属性变化越少，压缩比例越大，适合于类型区域面积较大的栅格。

    - 优点：
        1. 栅格加密时，数据量不会明显增加，压缩效率高，最大限度保留原始栅格结构，
        2. 编码解码运算简单，且易于检索、叠加、合并等操作，得到广泛应用。
    - 缺点：不适合于类型连续变化或类型区域分散的数据。


3. 块状编码

    ![](https://img-blog.csdnimg.cn/20190420112711673.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RhbkJvX0M=,size_16,color_FFFFFF,t_70)

    对大而简单的多边形更为有效，在合并、插入、检查延伸性、计算面积等操作时有明显的优越性

4. 四叉树编码

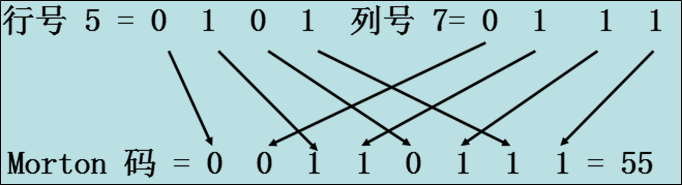
    **莫顿码**

    十进制莫顿码产生过程：十进制的行、列坐标表示为二进制，按位交错，得到二进制再转化为十进制。

    1. 四叉树编码

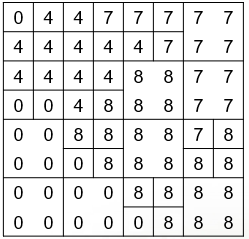
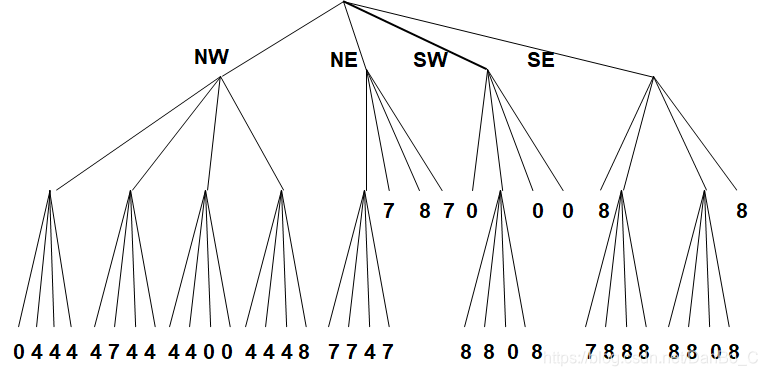
        ![](https://img-blog.csdnimg.cn/20190420112725786.png)
        ![](https://img-blog.csdnimg.cn/20190420112759775.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RhbkJvX0M=,size_16,color_FFFFFF,t_70)

        - 图形必须为2n×2n的栅格阵列。
        - n 为极限分割次数
        - n＋1是四叉树最大层数或最大高度


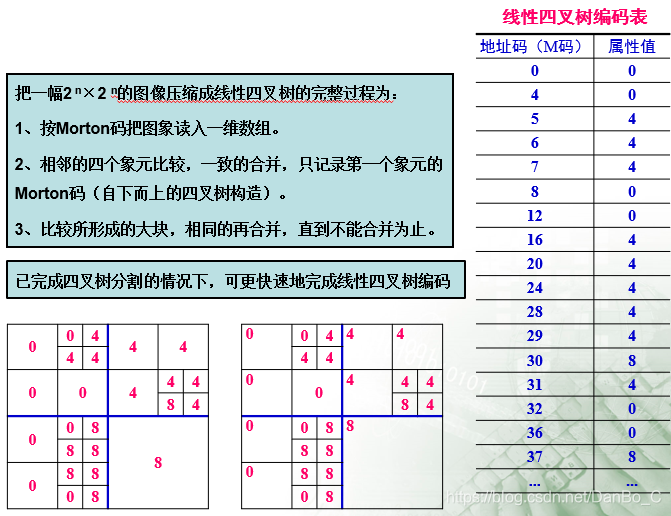
    2. 线性四叉树编码

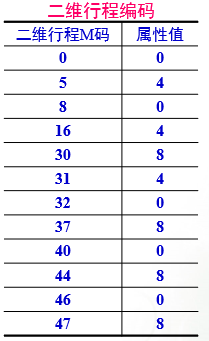
        ![](https://img-blog.csdnimg.cn/2019042011281168.png)
        ![](https://img-blog.csdnimg.cn/20190420112822376.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RhbkJvX0M=,size_16,color_FFFFFF,t_70)

    3. 二维行程编码

        ![](https://img-blog.csdnimg.cn/20190420112836674.png)
    4. 带指针的二维行程编码

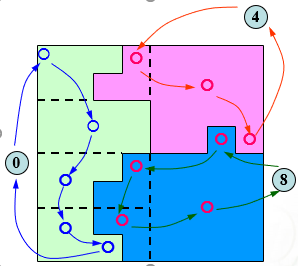
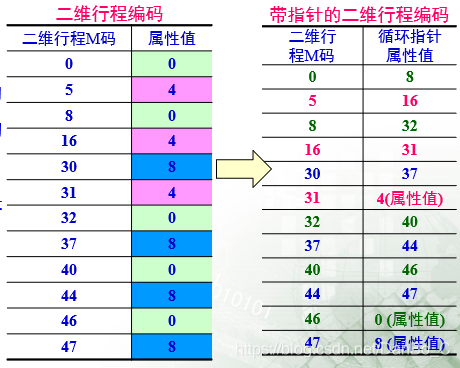
        ![](https://img-blog.csdnimg.cn/20190420112849656.png)
        ![](https://img-blog.csdnimg.cn/20190420112900448.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RhbkJvX0M=,size_16,color_FFFFFF,t_70)

    优点：有效地计算多边形的数量特征

    缺点：
    - 矢/栅正反变换还不理想
    - 建立四叉树耗时
    - 修改麻烦
    - 不直接体现物体之间的拓扑关系
    - 滑动变异
    - 失去了内在的相关性

5. 链式编码

    ![在这里插入图片描述](https://img-blog.csdnimg.cn/20190420112915384.png)
    ![](https://img-blog.csdnimg.cn/20190420112924164.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RhbkJvX0M=,size_16,color_FFFFFF,t_70)
    ![](https://img-blog.csdnimg.cn/20190420112940480.jpg?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RhbkJvX0M=,size_16,color_FFFFFF,t_70)

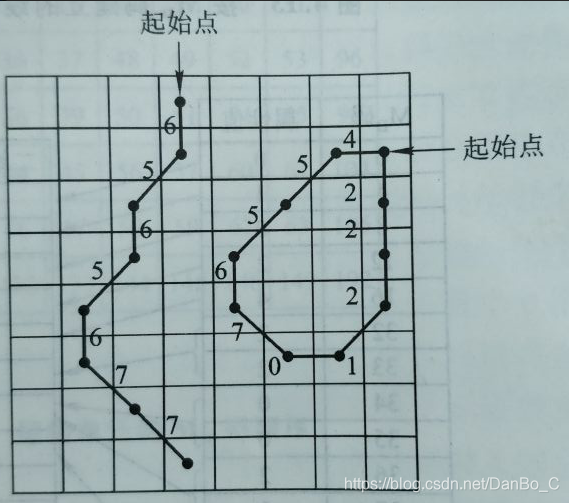
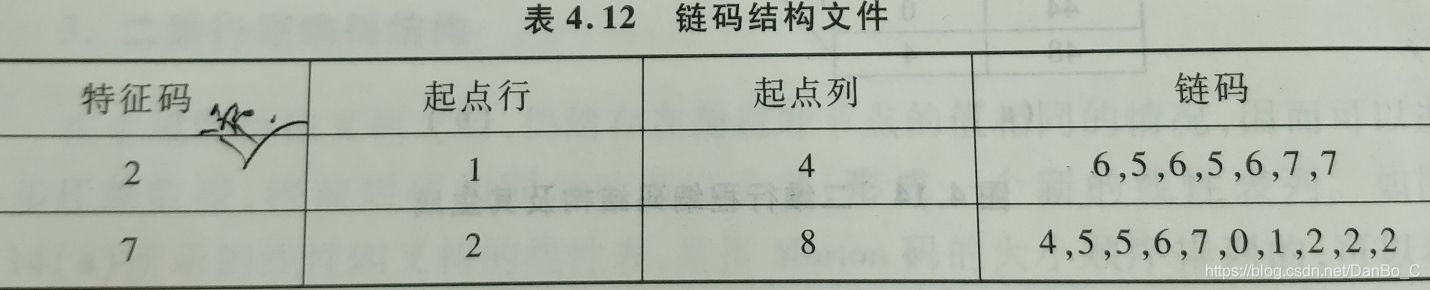8、矢量数据结构**

地理实体
- 点实体：具有特定的位置而没有长度的实体
- 线实体：具有长度的实体
  
  特征：
  - 长度：从起点到终点的总长；
  - 弯曲度：用于表示像道路拐弯时弯曲的程度。
  - 方向性：如水流方向,上下游; 公路,单双向之分。
- 面状实体：又称为多边形、区域等，水对湖泊、岛屿、地块等一类现象的描述
地理实体需要描述的内容：
- 编码
- 位置
- 类型
- 行为
- 属性
- 说明
- 时间维描述
- 关系
矢量数据结构定义

通过记录坐标的方式尽可能精确地理实体，坐标空间设为连续，允许任意位置、长度和面积的精确定义。特点：定位明显，属性隐含
获取方式
- 外业测量
- 栅格数据转换
- 跟踪数字化
组织方式
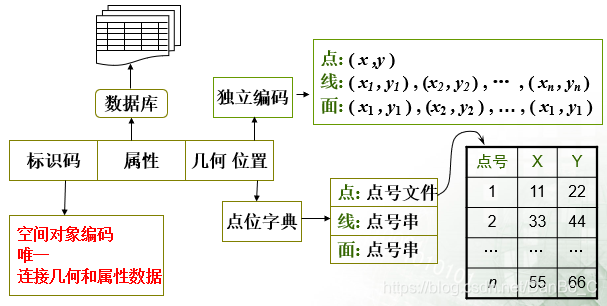
多边形矢量编码
1. 实体式数据结构
  
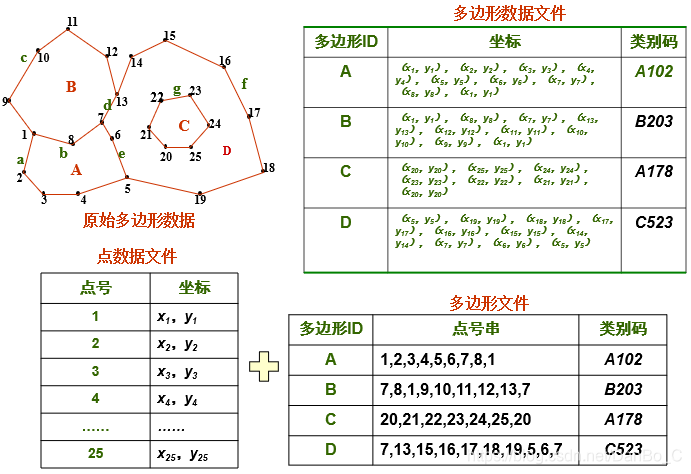
  只记录空间对象的位置坐标和属性信息，不记录拓扑关系
  
  优点：
```
结构简单、直观、易实现
```
  缺点：
  - 相邻多边形的公共边界被数字化并存储两次
  - 缺少多边形的邻接信息
  - 处理岛或洞等嵌套问题较麻烦
    区别于矢量的简单数据结构,矢量的拓扑空间数据结构的特点是：
    
    点是相互独立的，点连成线，线构成面；
    
    每条线始于起始结点，止于终止结点，并与左右多边形相邻接。
    
    矢量的拓扑空间数据结构主要有：
    - 索引式
    - 双重独立编码结构
    - 链状双重独立编码结构等。

2. 索引式数据结构    

    将坐标对以顺序方式存储，由点索引与边界线号相联系，以线索引与各多边形相联系，形成树状索引结构
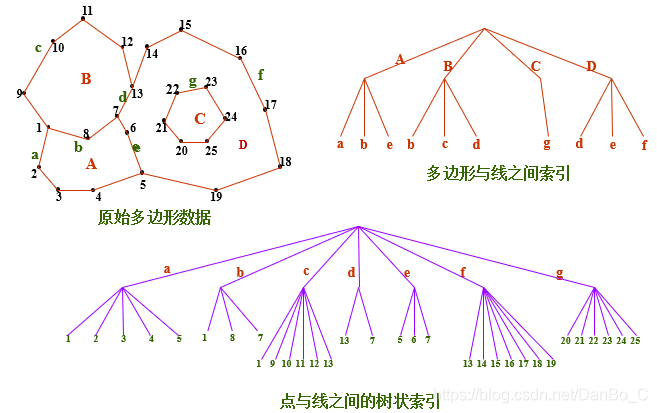
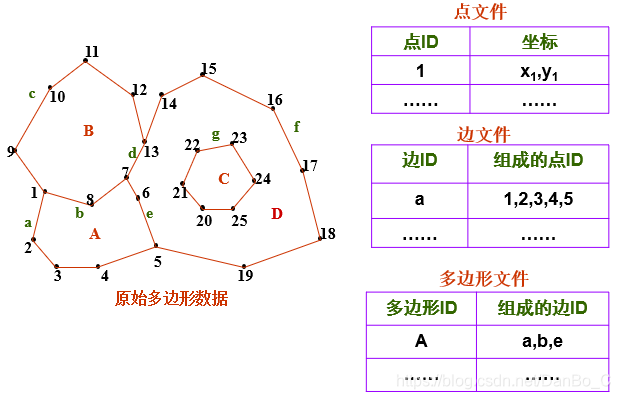
    ![](https://img-blog.csdnimg.cn/20190420113037878.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RhbkJvX0M=,size_16,color_FFFFFF,t_70)
    ![](https://img-blog.csdnimg.cn/20190420113047593.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RhbkJvX0M=,size_16,color_FFFFFF,t_70)

    - 优点：
        1. 消除数据的冗余和不一致 
        2. 邻接信息、岛信息可通过查找公共弧段号查询
    - 缺点：
        1. 表达拓扑关系繁琐
        2. 以人工建立编码表，工作量大，易出错

3. 双重独立式（DIME）
    美国人口统计局研制用来进行人口普查分析和制图的，以城市街道为编码的主体
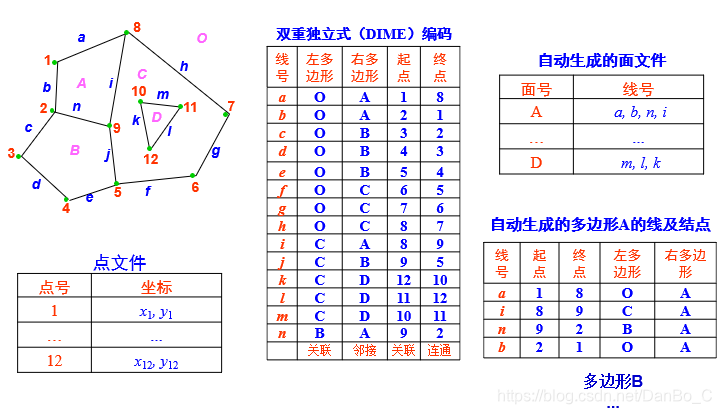
    ![](https://img-blog.csdnimg.cn/20190420113058805.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RhbkJvX0M=,size_16,color_FFFFFF,t_70)
    - 结点与结点或面域与面域之间是邻接关系。
    - 节点与线段或面域与线段之间为关联关系。

4. 链式双重独立式
    将若干直线段合为一个弧段(或链段)，每个弧段可以有许多中间点。 
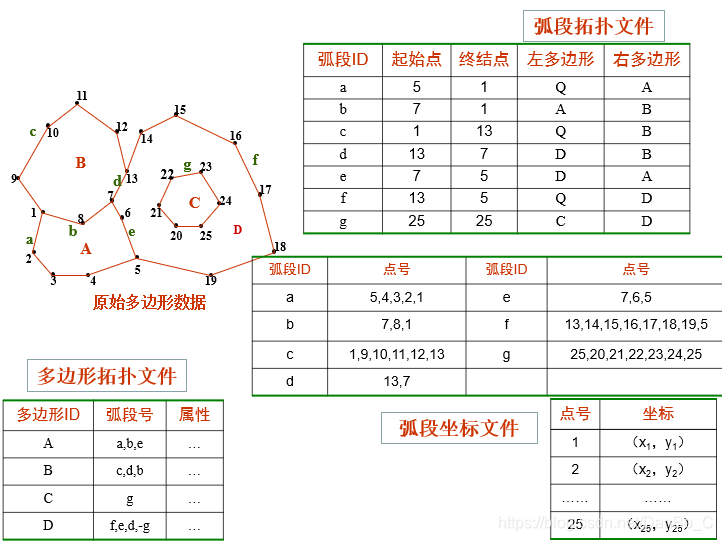
    ![](https://img-blog.csdnimg.cn/20190420113109643.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RhbkJvX0M=,size_16,color_FFFFFF,t_70)

    特点：拓扑关系明确，也能表达岛信息，而且以弧段为记录单位，满足实际应用需要。

9、矢量与栅格的比较与选择**

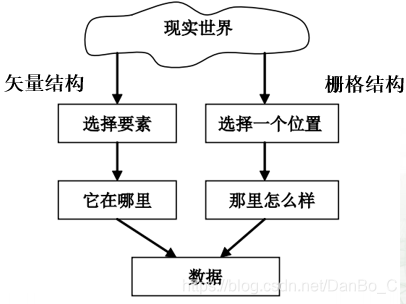
选择的原则：
- 要素还是位置
- 可获取的数据
- 定位要素的必要精度
- 需要什么类型的要素
- 需要什么类型的拓扑关系
- 所需空间分析类型
- 生产地图类型
栅格结构：大范围小比例尺的自然资源、环境、农林业等区域问题的研究。
矢量结构：城市分区或详细规划、土地管理、公用事业管理等方面的应用。

10、矢栅一体化

概念
- 将矢量面向目标的方法和栅格象元充填的方法结合起来，采用填满线状目标路径和充填面状目标空间的方法作为一体化数据结构的基础
- 点、线、面状地物均采用面向目标的描述方法，因此它保持了矢量的特性，而象元空间充填表达建立了位置与地物的联系，使之具有栅格的性质。
- 以矢量的方式来组织栅格数据的数据结构。
三个约定
- 点状地物仅有空间位置，没有形状和面积，在计算机内部仅有一个位置数据。
- 线状地物有形状但没有面积，在计算机内部需要用一组象元填满整个路径。
- 面状地物具有形状和面积，在平面上的投影是由边界包围的空间和一组填满路径的象元表达的边界组成。
细分网格法

一体化数据结构是基于栅格的，表达目标的精度受栅格尺寸的限制，可利用细分格网法提高数据的表达精度。
矢栅一体化数据结构设计 **
- 线性四叉树(Morton)是基本数据格式
- 三个约定作为设计点、线、面数据结构的基本依据
- 细分格网法保证足够精度。

11、镶嵌数据结构

**.采用规则或不规则的小面块集合来逼近自然界不规则的地理单元，适合于对连续变化场景的地理现象进行抽象。

**.小面块之间不重叠且能完整铺满整个地理空间。

**.分为规则镶嵌数据模型和不规则镶嵌数据模型。

规则镶嵌数据模型*

用规则的小面块集合来逼近自然界不规则的地理单元。
在实际应用中，普遍采用正方形或矩形进行地理空间的划分。此时的规则镶嵌数据模型就转化为栅格数据模型。
不规则镶嵌数据模型
- 有限离散的观测样点来表示某地理现象的空间分布规律时，适合于采用不规则镶嵌数据模型。
  - 最典型的不规则镶嵌数据模型有Voronoi图（也称Thiessen多边形）和不规则三角网（Triangular IrregularNetwork，简称TIN）模型。
1. Thiessen多边形构造**
  1. 样本点之间最近样本点的连线。
    - 最邻近的点
    - 外接圆范围内不含有其它离散点
    - 凸四边形
  2. 对每个三角形作中垂线。
  3. 相邻三角形外心（外接圆圆心）的连线或三角形边垂直平分线与图廓线构成泰森多边形。泰森多边形和Delaunay三角网互为偶图。
  4. 特征
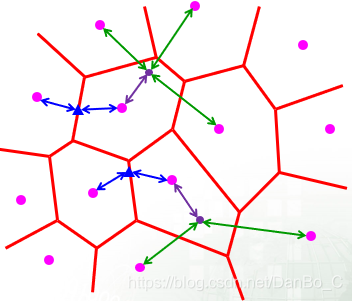
    - 每个泰森多边形内仅含有一个离散点；
    - 组成多边形的边总是与两相邻样点的连线垂直，泰森多边形内的点到相应离散点的距离最近；
    - 泰森多边形边上的点到其两边的离散点的距离相等。

2. 不规则三角网

    - 三角形大小随样点密度的变化自动变化，所有样点都称为三角形的顶点，当样点密集时生成的三角形小，而样点较稀时则三角形较大。
    - 任何一个Delaunay三角形的外接圆不能包含其他任何点在该包围的内部。

12、三维数据结构*

栅格：将地理实体的三维空间分成细小单元——体元。普遍用八叉树 **
矢量：x，y，z，抽象为点、线、面、体，面构成体。 **常用三维边界表示

八叉树结构
依次递归运算，直到每个子区域均为单一值为止。
三维边界表示法
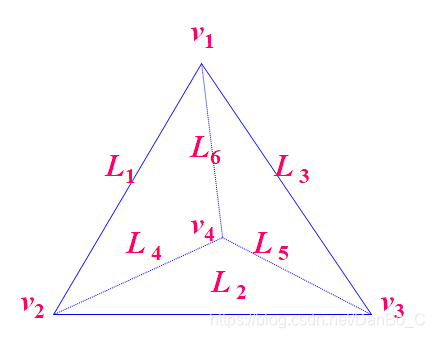
- 顶点表：用来表示多面体各顶点的坐标
- 边表：指出构成多面体某边的两个顶点